绍兴网站建设 微德福2023年6月疫情恢复
目录
二叉树的链式存储结构：：
1.创建一颗二叉树
2.二叉搜索树简介
3.前序、中序以及后序遍历
4.层序遍历
5.求一棵树的节点个数代码实现
6.求一棵树的高度代码实现
7.求叶子节点个数代码实现
8.求第K层节点个数代码实现
9.二叉树查找值为x的节点
二叉树的链式存储结构：：
1.创建一颗二叉树
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
BTNode* CreateTree()
{BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));assert(n1);BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));assert(n2);BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));assert(n3);BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));assert(n4);BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));assert(n5);BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));assert(n6);n1->data = 1;n2->data = 2;n3->data = 3;n4->data = 4;n5->data = 5;n6->data = 6;n1->left = n2;n1->right = n4;n2->left = n3;n2->right = NULL;n4->left = n5;n4->right = n6;n3->left = NULL;n3->right = NULL;n5->left = NULL;n5->right = NULL;n6->left = NULL;n6->right = NULL;return n1;
}注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后续重点讲解。
2.二叉搜索树简介
二叉搜索树：
若它的左子树不为空，则左子树上的所有节点的值均小于它的根节点的值，若它的右子树不空，
则右子树上所有节点的值均大于它的根节点的值，它的左右子树也分别为二叉排序树，二叉搜索树
作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点又有数组快速查找的优势，所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作，因此，二叉搜索树的增删查改才有意义，普通二叉树的增删查改价值不大。
3.前序、中序以及后序遍历
学习二叉树结构，最简单的方式就是遍历，所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树的节点进行相应的操作，并且每个节点只操作一次。访问节点所做的操作依赖于具体的应用问题。遍历是二叉树最重要的运算之一，也是二叉树上进行其他运算的基础。
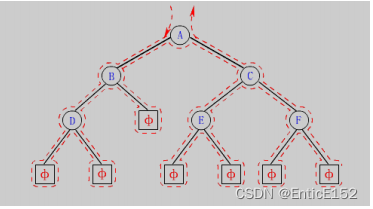
按照规则，二叉树的遍历有：前序、中序、后序的递归结构遍历：
1.前序遍历(PreOrder Traversal 亦称先序遍历)：访问根节点的操作发生在遍历其左右子树之前
2.中序遍历(InOrder Traversal)：访问根节点的操作发生在遍历其左右子树之间
3.后序遍历(PostOrder Traversal)：访问根节点的操作发生在遍历其左右子树之后
由于被访问的节点必是某子树的根，所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树、根的右子树。NLR、LNR、LRN分别又称为先根遍历、中根遍历和后根遍历。
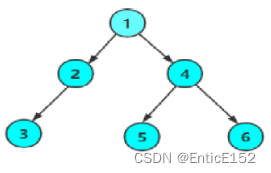
前序遍历结果：1 2 3 4 5 6
中序遍历结果：3 2 1 5 4 6
后序遍历结果：3 2 5 6 4 1
前序遍历递归图解：
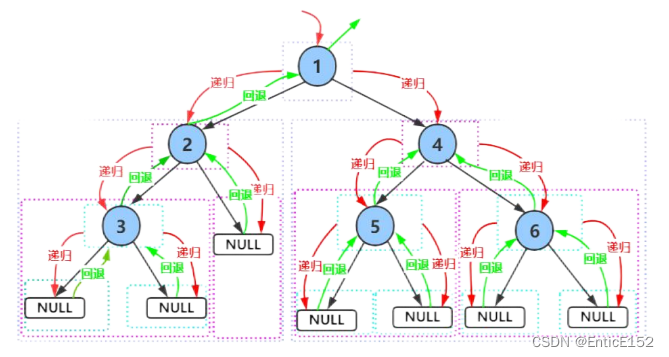
//二叉树的前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
//二叉树的中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
//二叉树的后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}4.层序遍历
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层
上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
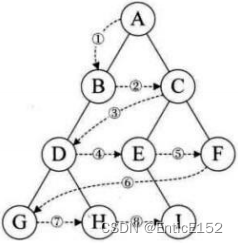
//层序遍历
//利用队列的性质，将父亲节点入队列，出队列的时候，将其孩子入队列(上一层节点出的时候代入下一层)
//注:队列需要二叉树的节点定义，二叉树层序遍历需要队列，在此需要解决相互包含的问题，所以要将二叉树的节点定义放到Queue.h中
//复制粘贴队列代码
Queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
typedef BTNode* QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;
//第三种不用二级指针的方式 封装成结构体
typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;
void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
//取队列头部数据
QDataType QueueFront(Queue* pq);
//取队列尾部数据
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);
void TreelevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头数据 这里队列中的数据是指针BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);//下一层入队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestory(&q);
}
Queue.c
#include"Queue.h"
void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}
void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);}pq->head = pq->tail = NULL;
}
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}else{newnode->data = x;newnode->next = NULL;}if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);del = NULL;}pq->size--;
}
//取队列头部数据
QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}
//取队列尾部数据
QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}
int QueueSize(Queue* pq)
{assert(pq);/*QNode* cur = pq->head;int n = 0;while (cur){++n;cur = cur->next;}return n;*/return pq->size;
}
void TreelevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头数据 这里队列中的数据是指针BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);//下一层入队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestory(&q);
}选择题练习：
1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为（）
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为（）
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
答案：
A
A
D
A5.求一棵树的节点个数代码实现
//求一棵树的节点个数
//遍历计数的缺陷:
//静态成员变量只会在定义时初始化一次
int TreeSize(BTNode* root)
{static int count = 0;if (root == NULL)return count;++count;TreeSize(root->left);TreeSize(root->right);return count;
}
//遍历计数的缺陷:
//全局变量
//调用时依旧要注意 count初始化一下 因为生命周期在全局 作用域在这个函数
int count = 0;
void TreeSize(BTNode* root)
{if (root == NULL)return;++count;TreeSize(root->left);TreeSize(root->right);return;
}
int main()
{printf("Tree Size:%d\n", TreeSize(root));printf("Tree Size:%d\n", TreeSize(root));count = 0;TreeSize(root);printf("Tree Size:%d\n", root);count = 0;TreeSize(root);printf("Tree Size:%d\n", root);return 0;
}
//子问题思路解决
int TreeSize(BTNode* root)
{//注意:一定是TreeSize(root->left)和TreeSize(root->right)都返回值时，才+1在往上一层返回return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
6.求一棵树的高度代码实现
//求树的高度
//父亲的高度 = 左右子树的高度大的 + 1
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}7.求叶子节点个数代码实现
//求叶子节点的个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);}8.求第K层节点个数代码实现
//求第K层节点个数
//转换成求左右子树的第K-1层
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}//转换成求子树的第k-1层return Tree(root->left, k - 1) + TreeLevel(root->right, k - 1);
}
9.二叉树查找值为x的节点
//返回x所在的节点
//该代码是一个前序查找的过程
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}//一定要用返回值接收递归的结果 不然就要递归调用一次自己BTNode* leftRet = TreeFind(root->left, x);//先去左树找 找到了就返回if (leftRet != NULL){return leftRet;}//左树没有找到再到右树找BTNode* rightRet = TreeFind(root->right, x);if (rightRet != NULL){return rightRet;}return NULL;
}
代码简化：
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}//一定要用返回值接收递归的结果 不然就要递归调用一次自己BTNode* leftRet = TreeFind(root->left, x);//先去左树找 找到了就返回if (leftRet != NULL){return leftRet;}//递归右树 找到了就返回 找不到就返回NULLreturn TreeFind(root->right, x);
}