当前位置： 首页 > news >正文

嘉峪关市建设局公示公告网站亚马逊关键词排名查询工具

news 2025/7/2 5:03:06
嘉峪关市建设局公示公告网站,亚马逊关键词排名查询工具,怎么用 java做网站,青岛门户网站建设前言 作者：小蜗牛向前冲 名言：我可以接受失败，但我不能接受放弃 如果觉的博主的文章还不错的话，还请点赞，收藏，关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 目录 一、红黑树的…

前言

作者：小蜗牛向前冲

名言：我可以接受失败，但我不能接受放弃

  如果觉的博主的文章还不错的话，还请点赞，收藏，关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正

目录

一、红黑树的基本知识

 1、红黑树的概念

2、性质 

二、红黑树的模拟实现 

1、节点的定义

2、红黑树的插入 

三、红黑树的测试

1、验证的准备工作

2、测试用例 

3、完整代码实现 

四、AVL树和红黑树的比较 

本期学习目标：什么是红黑树，红黑树是怎么实现的，红黑树的测试，红黑树和AVL树的对比 

一、红黑树的基本知识

 1、红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路 径会比其他路径长出俩倍（最长路径吧会超过最短路径的2倍），因而是接近平衡的。

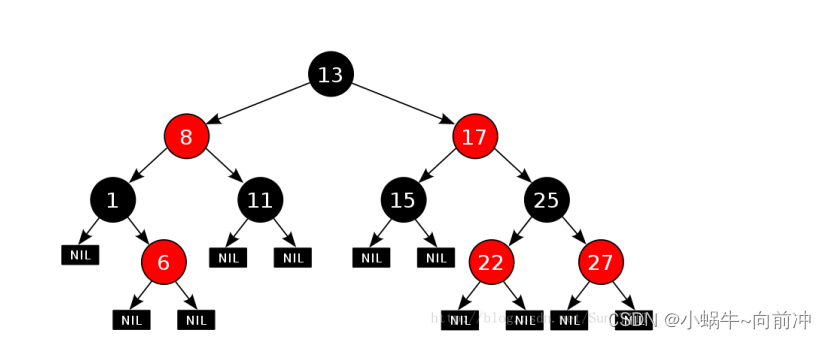
2、性质 

  1. 每个结点不是红色就是黑色。
  2.  根节点是黑色的 。
  3.  如果一个节点是红色的，则它的两个孩子结点是黑色的。(没有连续的红节点)
  4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点 。(每条路径下都包含相同的黑节点)
  5.  每个叶子结点都是黑色的(此处的叶子结点指的是空结点)。

 推论：

  1. 最短路径：全部由黑节点组成
  2. 最长路径：一黑一红，红节点数量 == 黑节点数量

这里我们思考一下，红黑树是如何保证：最长路径不超过最短路径的2倍？

  • 由推论2可知，对于最长路经，就是一红一黑，而且红节点数量等于黑节点数量，
  • 在由推论1可知，最短路径节点数量全为黑。
  • 在由性质4可知，每条路径的黑节点数量都相同，这就保证了最长路径不超过2倍的最短路径。

二、红黑树的模拟实现 

1、节点的定义

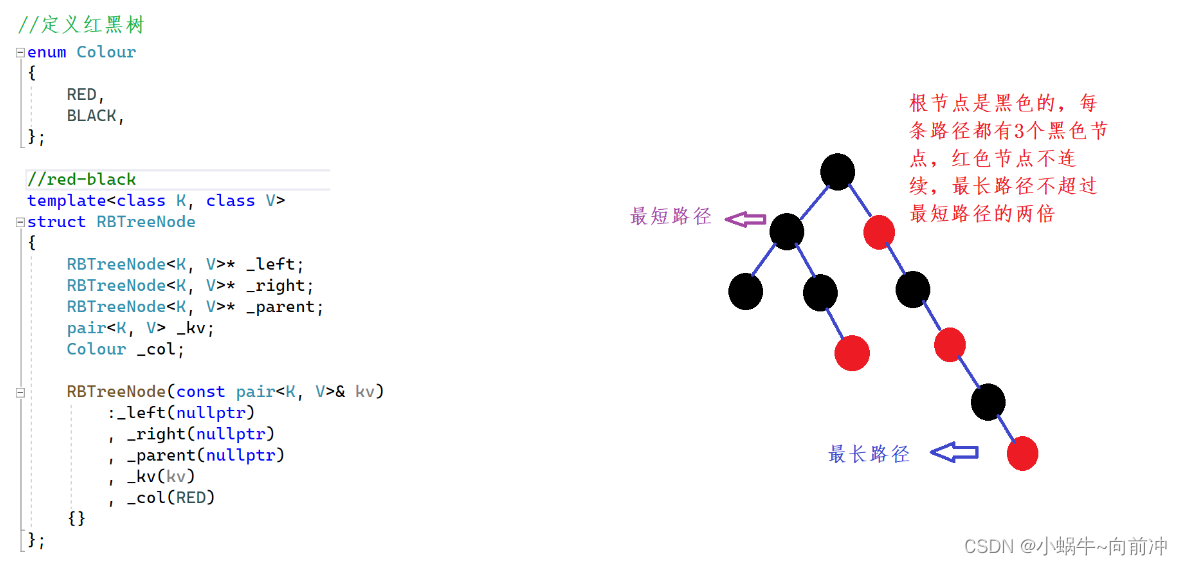
enum Colour
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};

2、红黑树的插入 

根据节点的定义，我们上面定义了一个枚举类型了存放显色的类型，RED和BLACK，但是我们在插入节点的时候是定义红色还是黑色呢？我们在上面定义的是红色为什么呢？

这里分类讨论一下：

定义新插入节点为黑色：

就会破坏性质4，导致每天路径的黑色节点数量不同

定义新插入节点为红色：

可能会破坏性质3，导致出现连续的红节点，但是这样也仅仅影响的是一条路径，影响有限。

综上所述：所以我们选择插入节点为红色。

红黑树是在二叉搜索树的基础上加上其平衡限制条件，因此红黑树的插入可分为两步：

1. 按照二叉搜索的树规则插入新节点

2.检测新节点插入后，红黑树的性质是否造到破坏

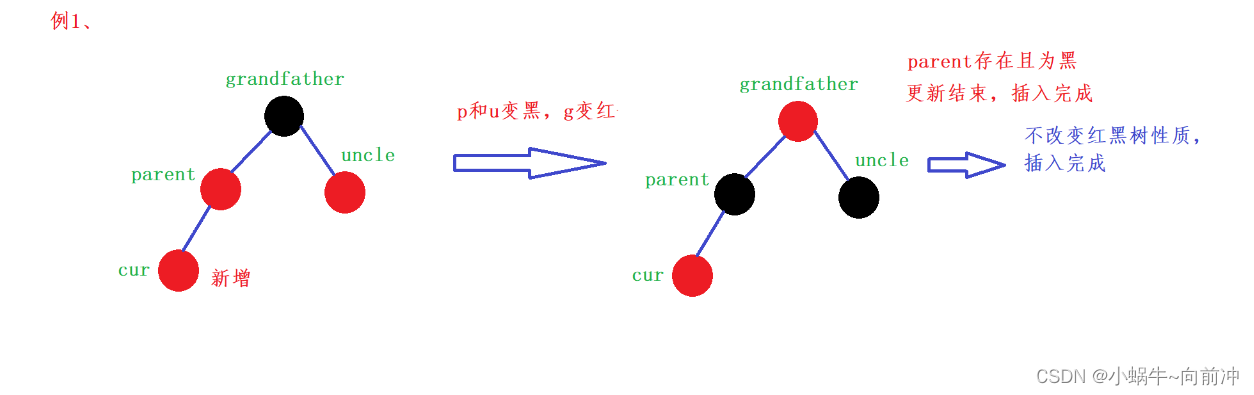
因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不需要调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连在一起的红色节点，此时需要对红黑树分情况来讨论：

约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点(p：parent g：grandfather u：uncle)

当p为g的左孩子时，有3种情况需要讨论

情况1：

 

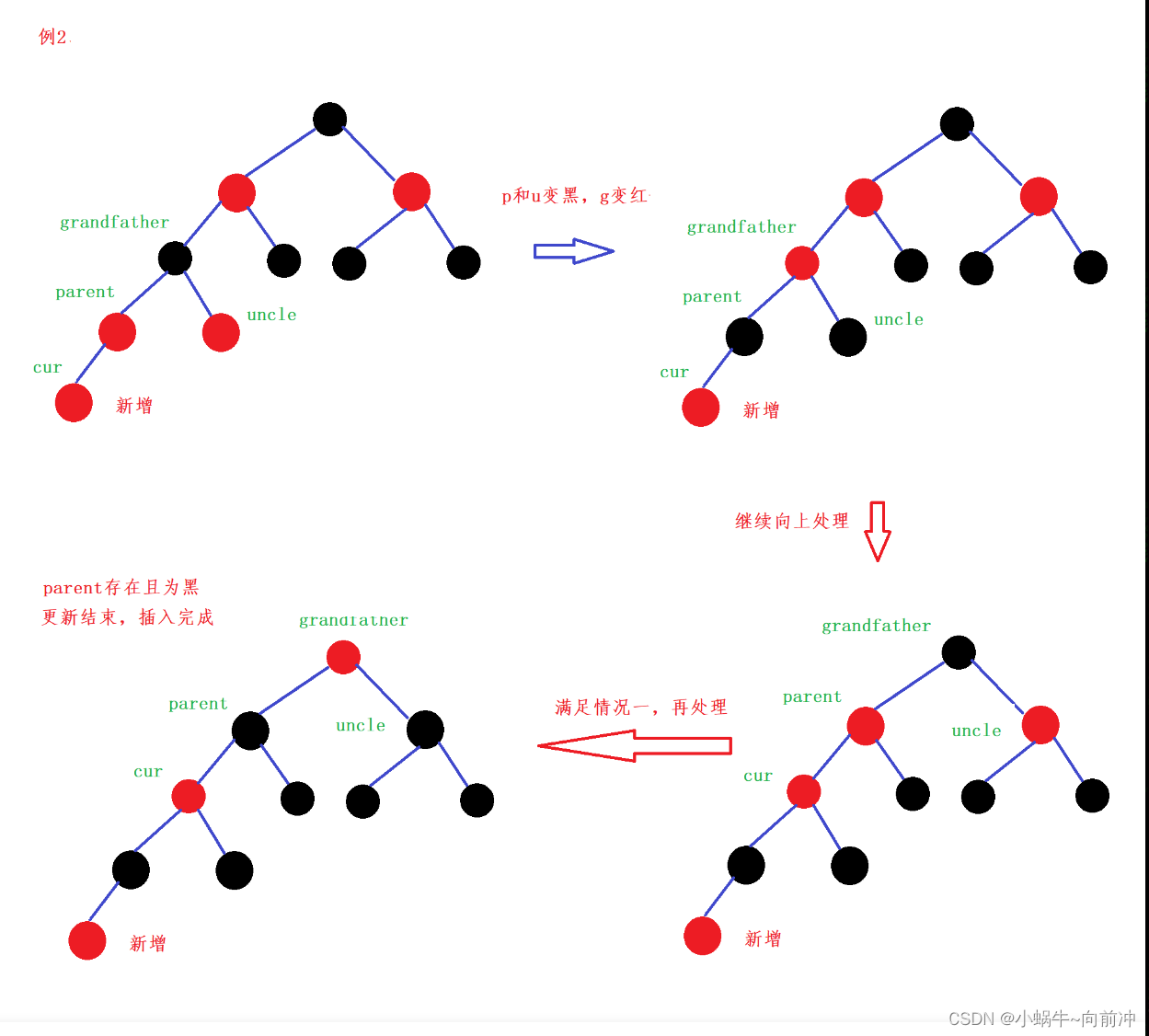
 情况2：

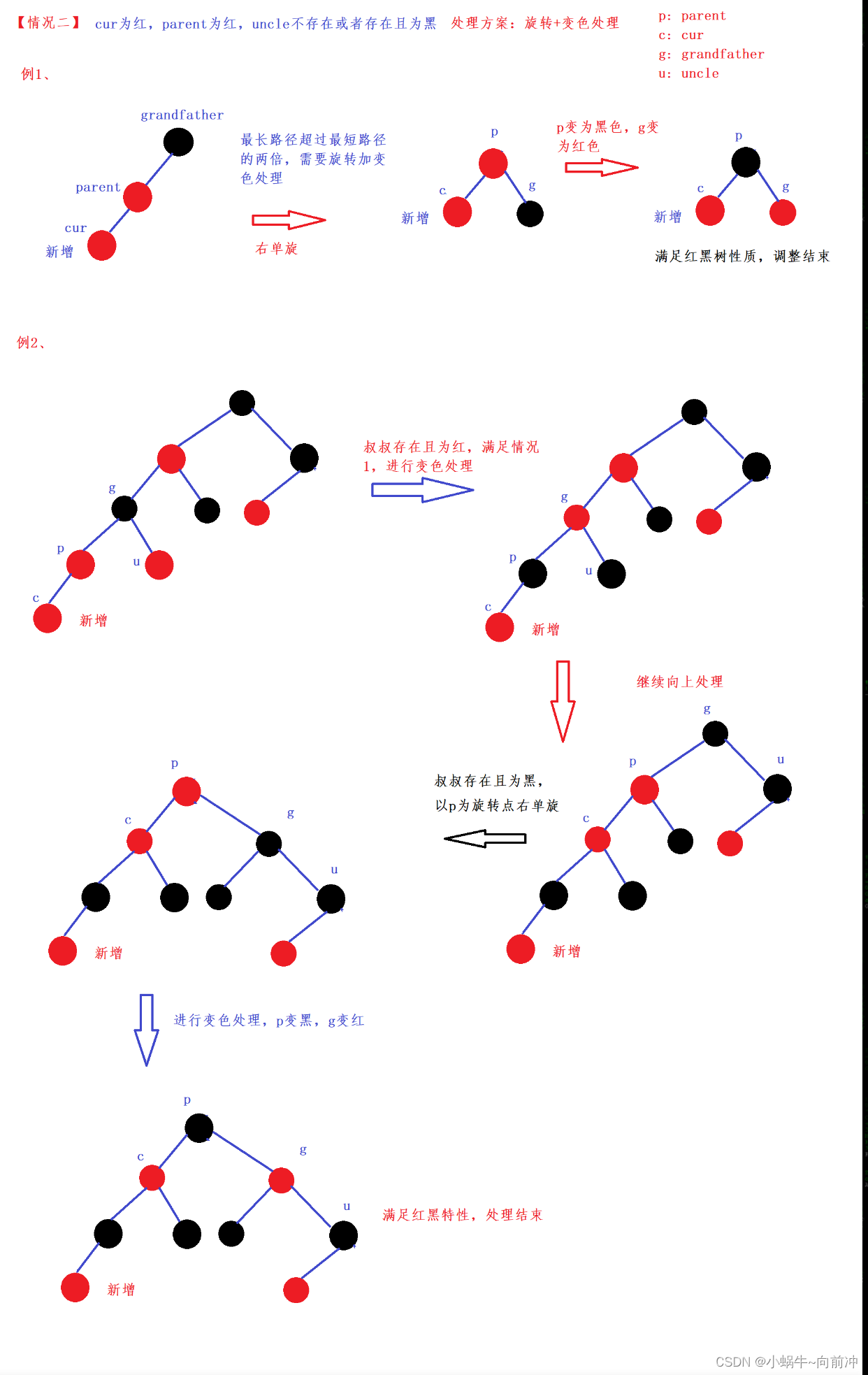
情况3：

 当p为g的右孩子时，也有3种情况需要讨论

这里的讨论和上面相似，处理方法也相似：

情况1：

情况2: 

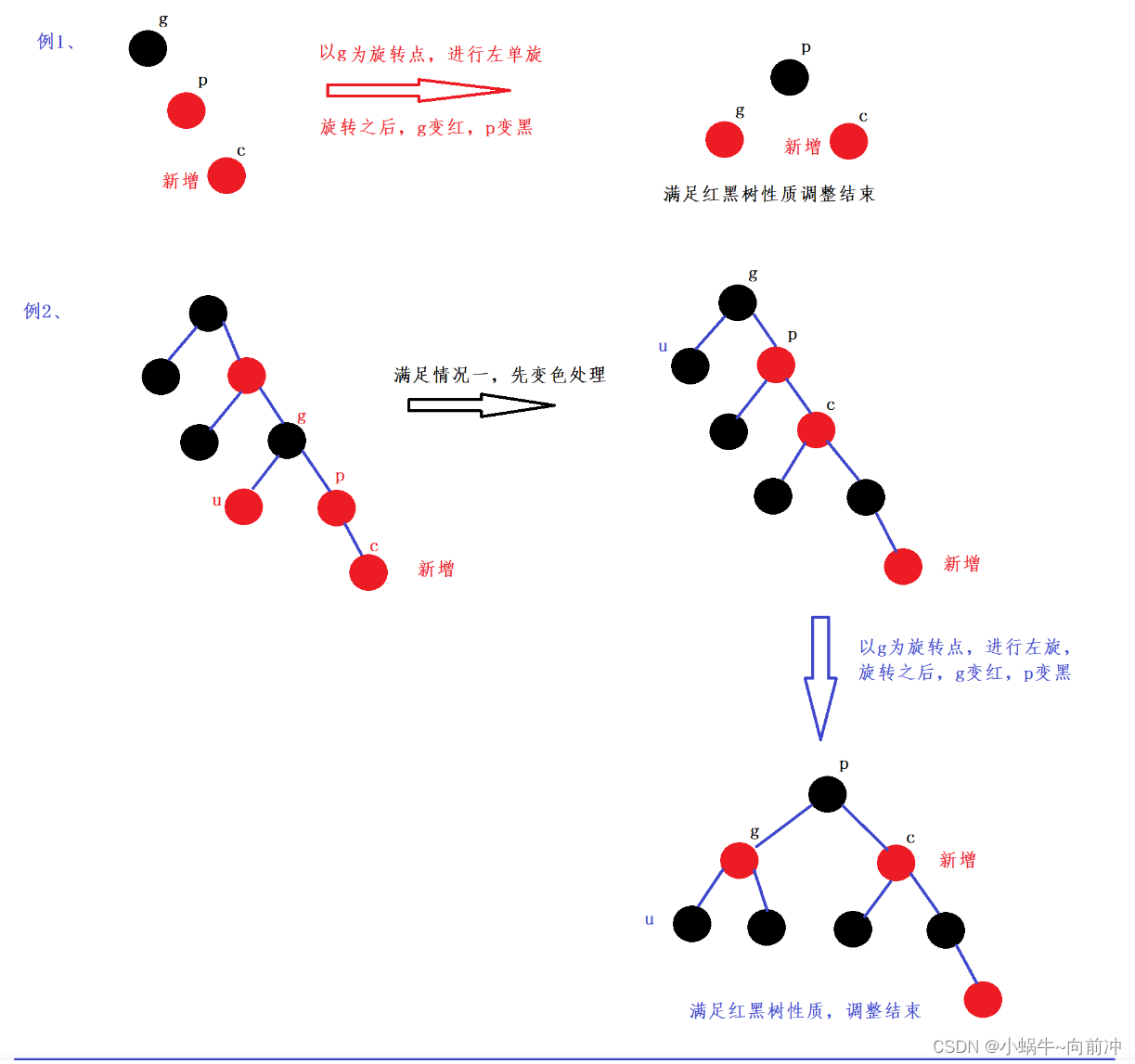
情况3：

代码实现：

bool insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找到插入位置Node* parent = nullptr;Node* cur = _root;while (cur){//到左子树找if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了cur = new Node(kv);cur->_col = RED;//默认颜色为红色//链接节点if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//插入后要调整红黑树//如果父亲存在且为红色while (parent && parent->_col == RED){Node* grandparent = parent->_parent;//情况1：cur为红色，p和u都为红色，g为黑色,这里的u是存在的//解决方法:p和n都变黑,g变红,在把cur当做g继续调整if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else//情况2+3  uncle存在且为黑色或者uncle不存在{if (cur == parent->_left){//情况2//解决方法:右单旋，将p变黑，g变红RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else//情况3：双旋转{RotateL(parent);RotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}//这里类比根节点为色，不需要在调整了break;}}else//grandparent->right == parent{//这里也是和上面一样分为三种情况Node* grandparent = parent->_parent;Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);//左单旋转parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}break;}}}//调整完成，把根节点变黑_root->_col = BLACK;return true;
}
//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* grandparent = parent->_parent;//让subLR变为parent的左,parent->_left = subLR;//这里要判断一下subLR不为空if (subLR){subLR->_parent = parent;}//parent变为subL的右subL->_right = parent;parent->_parent = subL;//parent就是为根if (grandparent == nullptr){_root = subL;subL->_parent = grandparent;}else{//parnet是上grandparent的左子树if (grandparent->_left == parent){grandparent->_left = subL;}else{grandparent->_right = subL;}subL->_parent = grandparent;}
}//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;//parnet为根,要更新根if (ppNode == nullptr){_root = subR;subR->_parent = ppNode;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}
}

三、红黑树的测试

1、验证的准备工作

  1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)

  2. 检测其是否满足红黑树的性质
    检测方法：
    1、根节点是黑色，否则不是红黑树
    2、当前节点是红色，去检测父亲节点，父亲节点也是红色，则不是红黑树
    3、以最左侧路径的黑色节点为基准，其它路径上的黑色节点与基准不相等，不是红黑树

 检验代码：

void Inorder()
{_Inorder(_root);
}void _Inorder(Node* root)
{if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);
}bool Check(Node* root, int blackNum, const int ref)
{if (root == nullptr){//已经递归到最深处进行,本路径的黑节点树和ref数量对比if (blackNum != ref){cout << "违反规则：本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则：出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);
}bool IsBalance()
{if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}//求出最左路节点有多少个黑节点int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);
}

2、测试用例 

这里我们借用上面AVL树的测试用例即可

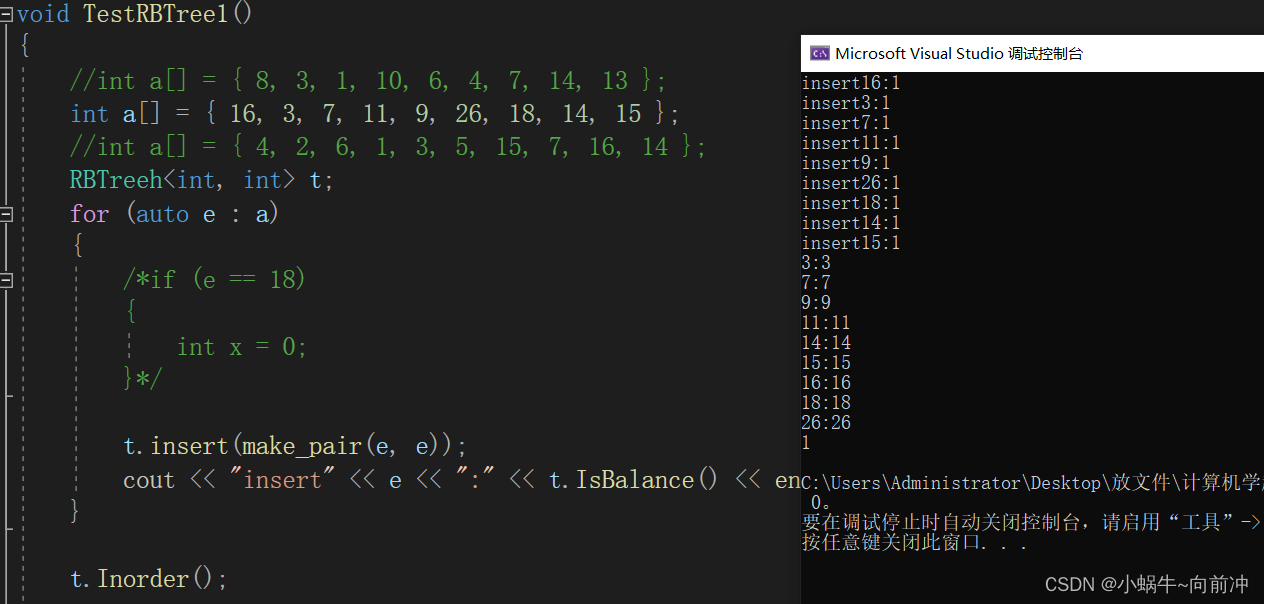
void TestRBTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTreeh<int, int> t;for (auto e : a){/*if (e == 18){int x = 0;}*/t.insert(make_pair(e, e));cout << "insert" << e << ":" << t.IsBalance() << endl;}t.Inorder();cout << t.IsBalance() << endl;
}void TestRBTree2()
{srand(time(0));const size_t N = 100000;RBTreeh<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand();t.insert(make_pair(x, x));//cout << t.IsBalance() << endl;}//t.Inorder();cout << t.IsBalance() << endl;
}

3、完整代码实现 

#pragma onceenum Colour
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};template<class K,class V>
class RBTreeh
{typedef RBTreeNode<K,V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找到插入位置Node* parent = nullptr;Node* cur = _root;while (cur){//到左子树找if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了cur = new Node(kv);cur->_col = RED;//默认颜色为红色//链接节点if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//插入后要调整红黑树//如果父亲存在且为红色while (parent && parent->_col == RED){Node* grandparent = parent->_parent;//情况1：cur为红色，p和u都为红色，g为黑色,这里的u是存在的//解决方法:p和n都变黑,g变红,在把cur当做g继续调整if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else//情况2+3  uncle存在且为黑色或者uncle不存在{if (cur == parent->_left){//情况2//解决方法:右单旋，将p变黑，g变红RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else//情况3：双旋转{RotateL(parent);RotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}//这里类比根节点为色，不需要在调整了break;}}else//grandparent->right == parent{//这里也是和上面一样分为三种情况Node* grandparent = parent->_parent;Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);//左单旋转parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}break;}}}//调整完成，把根节点变黑_root->_col = BLACK;return true;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* grandparent = parent->_parent;//让subLR变为parent的左,parent->_left = subLR;//这里要判断一下subLR不为空if (subLR){subLR->_parent = parent;}//parent变为subL的右subL->_right = parent;parent->_parent = subL;//parent就是为根if (grandparent == nullptr){_root = subL;subL->_parent = grandparent;}else{//parnet是上grandparent的左子树if (grandparent->_left == parent){grandparent->_left = subL;}else{grandparent->_right = subL;}subL->_parent = grandparent;}}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;//parnet为根,要更新根if (ppNode == nullptr){_root = subR;subR->_parent = ppNode;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}bool Check(Node* root, int blackNum, const int ref){if (root == nullptr){//已经递归到最深处进行,本路径的黑节点树和ref数量对比if (blackNum != ref){cout << "违反规则：本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则：出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}//求出最左路节点有多少个黑节点int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);}
private:Node* _root = nullptr;};void TestRBTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTreeh<int, int> t;for (auto e : a){/*if (e == 18){int x = 0;}*/t.insert(make_pair(e, e));cout << "insert" << e << ":" << t.IsBalance() << endl;}t.Inorder();cout << t.IsBalance() << endl;
}//void TestRBTree2()
//{
//	srand(time(0));
//	const size_t N = 100000;
//	RBTreeh<int, int> t;
//	for (size_t i = 0; i < N; ++i)
//	{
//		size_t x = rand();
//		t.insert(make_pair(x, x));
//		//cout << t.IsBalance() << endl;
//	}
//
//	//t.Inorder();
//	cout << t.IsBalance() << endl;
//}

四、AVL树和红黑树的比较 

AVL树（Adelson-Velsky and Landis tree）和红黑树都是自平衡的二叉搜索树，它们在维持树的平衡性上采用了不同的策略。以下是它们之间的一些比较：

  1. 平衡性维护策略：

    • AVL树： 通过保持任意节点的左右子树的高度差（平衡因子）不超过1来维护平衡。在每次插入或删除操作后，可能需要旋转来恢复平衡。
    • 红黑树： 通过引入额外的颜色信息和一些规则，确保树的高度保持在较小的范围内。具体来说，红黑树的平衡性维护是通过节点的颜色和一些颜色约束来实现的。

  2. 平衡因子和颜色信息：

    • AVL树： 使用平衡因子（Balance Factor）来表示每个节点左右子树的高度差。通常，平衡因子为 -1、0、1。
    • 红黑树： 使用颜色信息（红色或黑色）来表示树的平衡状态。通过遵循红黑树的性质，确保了树的平衡。

  3. 旋转操作：

    • AVL树： 插入或删除可能需要执行多次旋转操作，包括左旋、右旋、左右旋、右左旋等。
    • 红黑树： 插入或删除通常只需要执行一到两次旋转操作，因为红黑树引入了颜色信息，更灵活地维持平衡。

  4. 性能影响：

    • AVL树： 由于 AVL 树对平衡的要求更为严格，因此在插入和删除等操作时可能会导致更多的旋转，相对来说更耗费性能。
    • 红黑树： 由于其相对宽松的平衡条件，红黑树在插入和删除等操作时通常执行的旋转较少，因此性能可能相对更好。

  5. 应用场景：

    • AVL树： 适用于对搜索性能有较高要求的场景，例如在数据库中需要快速检索数据。
    • 红黑树： 通常在需要高效的插入和删除操作的情况下使用，例如在集合类的实现中。

总体而言，选择 AVL 树还是红黑树取决于应用的特定需求。如果搜索操作远远超过插入和删除，可能更倾向于使用 AVL 树。而在插入和删除操作频繁的情况下，红黑树可能更为适用。

http://www.qdjiajiao.com/news/7523.html

相关文章：

  • 电子工厂网站建设网店推广策划方案
  • 网站做sem优化抖音搜索优化
  • 制作书签沈阳企业网站seo公司
  • 网站使用功能介绍是用什么软件做的有道搜索引擎入口
  • flashfxp链接网站合肥网
  • 北京旅游网站建设开车搜索关键词
  • 外贸服装网站建设全国疫情高峰感染进度
  • 下载做蛋糕网站网络营销百科
  • 步骤的近义词莆田百度seo公司
  • 知乎 做网站的公司 中企动力seo作弊
  • 网站后台重置密码怎么做seo岗位
  • 企业网站设计制作收费软文推荐
  • html做简单网站实例全网营销推广方案
  • 做册子模板素材有哪些网站哪有网页设计公司
  • 网站建设业务员培训网络营销推广公司有哪些
  • 用自己的服务器做网站怎么制作个人网站
  • 世界知名网站seo点击排名软件哪家好
  • 怎么网站制作商铺营销推广方案
  • 响应式网站和网站seo重庆
  • 安徽建设厅网站地址厦门人才网唯一官方网站
  • 用自己的手机做网站百度一下就会知道了
  • 可以做装修效果图的网站有哪些友情链接有哪些
  • 网站制作设计教程凌哥seo技术博客
  • 网上赚钱靠谱吗seo搜索引擎优化服务
  • 包装设计效果图电商关键词排名优化怎么做?
  • 网站开发南城科技大厦微信管理
  • 小程序网站开发公司网络营销企业网站推广
  • wordpress 小说插件seo是什么seo怎么做
  • 建设自己的企业网站需要什么资料seo公司上海牛巨微
  • 塑料袋销售做哪个网站推广好软文推广公司有哪些