给网站做推广一般花多少钱东莞网络优化服务商

🔥个人主页：Quitecoder

🔥专栏：算法笔记仓

朋友们大家好啊，本篇文章我们来到算法的双指针的第二部分

1.有效三角形的个数

题目链接：611. 有效三角形的个数
题目描述：

这道题当然可以暴力求解，三层循环枚举所有情况，来进行判断，但是可以进行优化：

我们知道，三角形的满足条件是任意的两边之和大于第三边，但是如果我们已经判断了较小的两个边大于第三边，就不需要再进行剩下两组的判断，所以我们先进行排序，再进行枚举：

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());}
};

具体讲解一下我们的思路：

这里使用的是一种双指针技术：固定最长的边（也就是数组中的最大值），使用两个指针来查找剩余部分中可能的两个较短边。如果找到了两个较短边的长度和大于最长边，那么这三者能构成一个三角形

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int count=0;for(int i=nums.size()-1;i>=2;i--){int lat=i-1,pre=0;while(pre<lat){if(nums[pre]+nums[lat]>nums[i]){count+=lat-pre;lat--;}else pre++;}}return count;}
};

它利用了一个重要的性质：如果你有三条边长分别为 a, b 和 c，且 a ≤ b ≤ c，那么 a, b 和 c 可以构成一个三角形当且仅当 a + b > c

步骤如下：

1. 对数组 nums 进行升序排序
2. 初始化计数器 count 为 0
3. 从后往前遍历数组（从最大值开始，下标为 i），我们将这个值作为潜在的最长边 c
4. 对于每一个 c，设置两个指针：pre 指针指向数组的开始（下标为 0），lat 指针指向 c 之前的元素（下标为 i - 1）
5. 当 pre 指针小于 lat 指针时：
   • 计算 nums[pre] 和 nums[lat] 的和，将这个和与 nums[i]（也就是当前的 c）进行比较
   • 如果 nums[pre] + nums[lat] > nums[i]，由于数组已经排序，所有在 pre 和 lat 之间的元素与 nums[lat] 的和都会大于 nums[i]，所以我们可以将 lat - pre 个三角形加到 count 上
   • 然后将 lat 向左移动一位（减小一点以寻找下一个可能的三角形）
   • 如果和小于等于 nums[i]，我们将 pre 向右移动一位（增大一点以寻找可能的三角形）
6. 当处理完所有的 c 后，返回 count 作为结果

本道题还是很简单的

2.查找总价格为目标值的两个商品

题目链接：LCR 179.查找总价格为目标值的两个商品
题目描述：

算法的具体思路：

1. 初始化两个指针，pre 指向数组的开始（索引 0），last 指向数组的末尾（索引 price.size() - 1）

vector<int> s1;
int last=price.size()-1;
int pre=0;

2. 进行一个 while 循环，在数组两端移动 pre 和 last 指针直到它们相遇。循环的条件是 pre < last，确保没有重复使用相同的元素。

3. 在每次循环中，计算两个指针指向的数的和，判断这个和与目标值 target 的关系：

   • 如果和大于 target，那么为了减小和，last 指针左移（减小索引值）
   • 如果和小于 target，那么为了增大和，pre 指针右移（增加索引值）
   • 如果和等于 target：
     • 将这两个数添加到结果 vector s1 中。
     • 因为只需要一组解，所以找到一对满足条件的数之后，通过 break 语句退出循环

while(pre<last)
{if(price[pre]+price[last]>target)last--;else if(price[pre]+price[last]<target)pre++;else {s1.push_back(price[pre]);s1.push_back(price[last]);break;}
}

4. 返回结果 vector。如果找到至少一对和为 target 的数，s1 会包含这两个数。如果没有找到，s1 将是空的

完整代码如下：

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {vector<int> s1;int last=price.size()-1;int pre=0;while(pre<last){if(price[pre]+price[last]>target)last--;else if(price[pre]+price[last]<target)pre++;else {s1.push_back(price[pre]);s1.push_back(price[last]);break;}}return s1;}
};

3.三数之和

题目链接：15.三数之和
题目描述：

对于三数之和，我们大思路如下：

对于示例
我们首先进行排序：

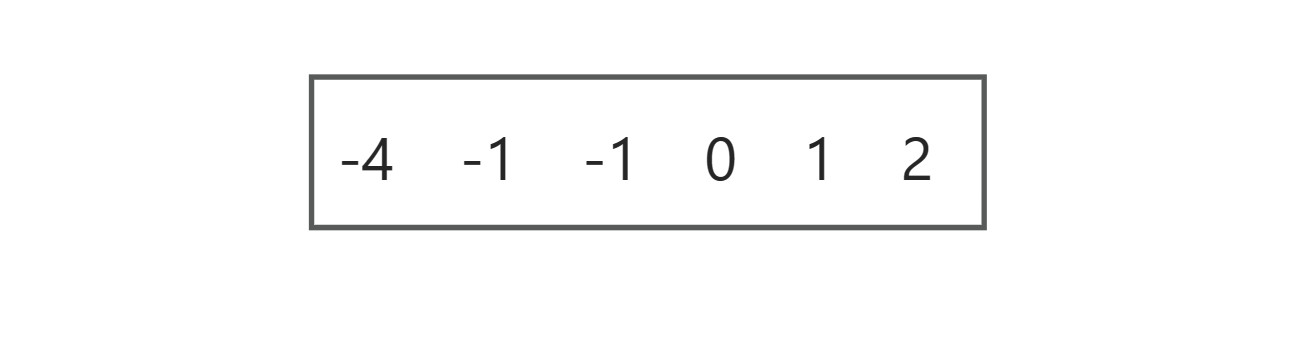
然后，首先固定第一个数，只需要在后面的数中找到两个数使三个数相加和为0即可

对于后面的数的寻找，我们可以设置前后指针，如果三数之和大于零，则让较大的数减小点，即右指针左移，三数之和小于零，则让左指针右移，如果等于零，则讲这三个数据插入到目标数组中继续遍历

注意，上面的{-1，0，1}这三个数是可以构成目标数的，但是必须跳过其中一个-1，因为不能重复

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> result;sort(nums.begin(),nums.end());for(int i=0;i<nums.size()-2;i++){if(i>0&&nums[i-1]==nums[i])continue;int pre=i+1,las=nums.size()-1;while(pre<las){if(nums[pre]+nums[las]<(-nums[i]))pre++;else if(nums[pre]+nums[las]>(-nums[i]))las--;else{result.push_back({nums[i],nums[pre],nums[las]});while(pre<las&&nums[pre+1]==nums[pre])pre++;while(pre<las&&nums[las-1]==nums[las])las--;pre++;las--;}}}return result;}
};

注意的要点：

1. 唯一性：返回的结果中不能包含重复的三元组。解决方法是在找到一个符合条件的组合后，跳过所有相同的元素

2. 遍历策略：外层循环遍历数组，内层使用双指针从两端向中间查找两个其他元素，以保证三个数的和为零

3. 跳过重复元素：

• 在外层循环中，如果当前的数字与前一个数字相同，则跳过以避免重复的三元组

 for(int i=0;i<nums.size()-2;i++)
{if(i>0&&nums[i-1]==nums[i])continue;

• 在找到一个满足条件的三元组之后，同时跳过 pre 指针的连续重复数字，并将 pre 指针向右移动
• 同样地，跳过 las 指针的连续重复数字，并将 las 指针向左移动

6. 寻找条件：三数之和等于零。这意味着在内层循环中，如果 nums[pre] + nums[las] 小于 -nums[i]，则需要右移 pre 指针；如果大于 -nums[i]，则需要左移 las 指针；如果等于 -nums[i]，则记录该三元组，继续寻找其他可能的组合

7. 边界条件：

   • 外层循环的循环变量 i 应小于 nums.size() - 2，因为需要至少3个数来组成一个三元组
   • 当 pre 和 las 指针相遇时，内层循环结束。

我们还可以进一步优化，当i对应的数字大于零，意味着无论如何结果都大于零，就可以直接break了：

for(int i=0;i<nums.size()-2;i++)
{if(i>0&&nums[i-1]==nums[i])continue;if(nums[i]>0)break;

4.四数之和

题目链接：18.四数之和
题目描述：

这道题与上面三数求和大体思路一样，我们这次一次固定两个数，然后再遍历剩下的数，遇见相同的数就往后移动

注意
上道题数组长度是大于等于3的，而这道题nums数组长度大于等于1，意味着可能不存在四个数，所以首先我们先判断数组长度，如果小于四直接返回空数组

if(nums.size()<4)return{};

首先进行排序工作

接着开始完成函数内容，需要固定两个数，我们则需要嵌套两个循环，注意边界值即可：

vector<vector<int>> result;
sort(nums.begin(), nums.end());
for(int i = 0; i < nums.size()-3; i++) {if (i > 0 && nums[i] == nums[i - 1]) continue; for (int j = i + 1; j < nums.size()-2; j++) {if (j > i + 1 && nums[j] == nums[j - 1]) continue; ——————————
}

这里处理逻辑与上面一样，先跳过相同的数，在j的循环中，我们就进行和上面相同的操作了

int pre = j + 1;
int last = nums.size() - 1;
while (pre < last) {long long sum = (long long)nums[i] + nums[j] + nums[pre] + nums[last]; if (sum < target) {pre++;}else if (sum > target) {last--;}else {result.push_back({ nums[i], nums[j], nums[pre], nums[last] });while (pre < last && nums[pre] == nums[pre + 1]) pre++; while (pre < last && nums[last] == nums[last - 1]) last--; pre++;last--;}
}

本题还有一个关键点

它提供的值不一定是整形，所以上面函数中我们使用长整型来避免溢出

总代码如下：

class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {if (nums.size() < 4)return{};vector<vector<int>> result;sort(nums.begin(), nums.end());for (int i = 0; i < nums.size() - 3; i++) {if (i > 0 && nums[i] == nums[i - 1]) continue; for (int j = i + 1; j < nums.size() - 2; j++) {if (j > i + 1 && nums[j] == nums[j - 1]) continue; int pre = j + 1;int last = nums.size() - 1;while (pre < last) {long long sum = (long long)nums[i] + nums[j] + nums[pre] + nums[last];if (sum < target) {pre++;}else if (sum > target) {last--;}else {result.push_back({ nums[i], nums[j], nums[pre], nums[last] });while (pre < last && nums[pre] == nums[pre + 1]) pre++;while (pre < last && nums[last] == nums[last - 1]) last--;pre++;last--;}}}}return result;}
};

5.双指针常见场景总结

双指针主要应用在有序数组或链表的问题中，以及一些可以通过前后关系来优化问题的场景：

1. 有序数组的对撞指针：

   • 两数之和：在有序数组中找到两个数，使它们的和为特定的目标值
   • 三数之和/四数之和：与两数之和类似，但需要找到三个或四个数的组合
   • 移除元素：从有序数组中移除重复项或特定值，并返回新数组的长度

2. 快慢指针：

   • 链表中环的检测：使用快慢指针检测链表是否有环，快指针一次移动两步，慢指针一次移动一步
   • 寻找链表中点：使用快慢指针找到链表的中间节点，快指针结束时慢指针在中点
   • 寻找链表的倒数第k个元素：快指针先移动k步，然后快慢指针共同移动，快指针到达末尾时慢指针所在位置即倒数第k个元素

3. 前后指针：

   • 归并排序中的合并步骤：使用两个指针分别指向两个有序数组的开始位置，以合并成一个新的有序数组。
   • 对链表进行操作：在链表上进行操作时，如删除节点或反转链表，常常需要前后指针来保持结点的连接。

4. 左右指针：

   • 二分查找：在有序数组中查找元素，使用左右指针限定查找范围

双指针方法的关键在于，指针的移动可以依据问题的规律来减少不必要的比较或计算，从而提高算法效率。当然，双指针的使用需要充分理解问题的性质，并巧妙设计指针的移动策略。在很多问题中，双指针技术都能将时间复杂度从 O(n²) 优化到 O(n),超级好用

本节内容到此结束！！感谢大家阅读！！