龙华区网站建设互联网营销是干什么

•  123.买卖股票的最佳时机III  

•  188.买卖股票的最佳时机IV 

第一题：买卖股票的最佳时机III  

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

• 示例 1:

• 输入：prices = [3,3,5,0,0,3,1,4]

• 输出：6 解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3。

就是说对于这个股票，只能进行最多四次操作，买了卖了然后再买再卖

动规五部曲

（1）确定dp数组以及下标的含义

一天可以发生5种情况

0. 没有操作

1.第一次持有股票

2.第一次不持有股票

3.第二次持有股票

4.第二次不持有股票

这里还是使用二维数组，但是之前只有dp[i][0]和dp[i][1]两种情况，这里dp[i][j]中表示第i天，j为[0-4]共5个状态，dp[i][j]表示第i天状态j所剩最大现金。

（2）确定递推公式

达到dp[i][1]状态，有两个具体的操作：

操作一：第i天买入股票，那么dp[i][1]=dp[i-1][0]-prices[i]

操作二：第i天没有操作，dp[i][1]=dp[i-1][1]

dp[i][1]=max(dp[i-1][0]-prices[i],  dp[i-1][1])；还是取最大的情况

dp[i][2]也有两种具体操作：

操作一：第i天卖出了股票，那么dp[i][2]=dp[i-1][1]+prices[i]

操作二：第i天没有卖出股票，跟前一天一样，dp[i][2]=dp[i-1][2]

同理，dp[i][2]=max(dp[i-1][1]+prices[i], dp[i-1][2]);

同上 dp[i][3]和dp[i][4]一样的计算方法

（3）dp数组如何初始化

第0天没有操作，即dp[0][0]=0

第0天做第一次买入的操作，即dp[0][1]=-prices[0]

第0天做第一次卖出的操作，因为没有股票，所以没有卖出的东西，dp[0][2]=0

同理，第二次买进卖出: dp[0][3]=-prices[0];  dp[0][4]=0

（4）确定遍历顺序

从前向后遍历

（5）举例推导dp数组

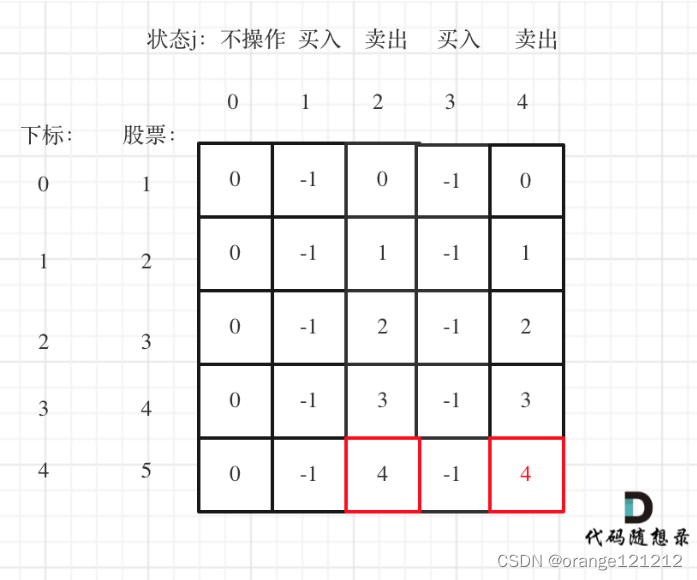
似乎有一些理解了：之前只能买进卖出各一次，所以对于i天来说，可以买进，或者卖出，dp[i][0]就是买进操作，dp[i][1]就是卖出操作，最后求出最大的值

第二题：买卖股票的最佳时机IV

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

• 示例 1：

• 输入：k = 2, prices = [2,4,1]

• 输出：2 解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2。

相比上一题，k成了可变的；

也就是进行k此买进，k次卖出；

其他规则和上题一样：

只要dp[i][j]的下标有了新的意义，int j=0;j<2*k-1;j++

为什么呢，因为k次交易，就一共是2k次动作，每一次都可以买（卖）或者不操作

//首先dp[0][0]不做操作为0//然后dp[0][1]表示第一次买进//dp[0][3]表示第二次买进，前面可能都没有操作，所以“第一次”买进的时候，钱为-prices[0];for(int j=1;j<2*k;j+=2){   dp[0][j]=-prices[0];}