金华市金东区建设局网站长沙互联网网站建设

二叉搜索树又称为二叉排序树，是一种具有一定性质的特殊的二叉树；

二叉搜索树的性质

若它的左子树不为空，则左子树上结点的值均小于根节点的值；
若它的右子树不为空，则右子树上结点的值均大于根节点的值；
二叉搜索树的左右子树均为二叉搜索树；

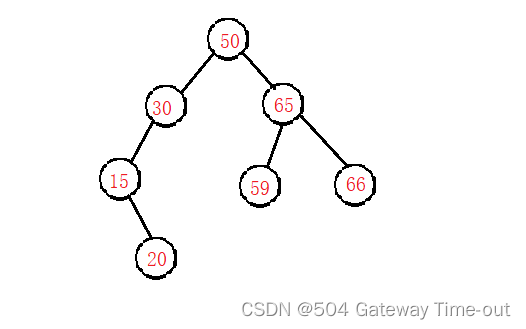
二叉搜索树的操作

遍历

关于二叉树的遍历方式有前序、中序、后序三种，对于二叉搜索树而言，使用中序遍历得到的结点序列是有序的；

public class BinarySearchTree {
//首先创建相关的结点结构static class TreeNode {public int key;public TreeNode left;public TreeNode right;TreeNode(int key){this.key=key;}}public TreeNode root;//进行中序遍历public void inorder(TreeNode root){if (root==null) return;inorder(root.left);System.out.println(root.key+" ");inorder(root.right);}
}

查找

基于二叉搜索树的性质，当根节点不为空时，可以根据根节点的值与待查找的值key之间的关系进行查找；即若根节点的值大于key，则在其左子树进行查找；若根节点的值小于key，则到其右子树进行查找；直到最终根节点的值为空或没有找到key则结束；

public TreeNode search(int key){//定义一个cur从根节点的位置开始查找TreeNode cur=root;while (cur!=null){//结点的值与key相等，找到并返回if (cur.key==key){return cur;}else if(cur.key<key){//结点的值小于key，去其右子树进行查找cur=cur.right;}else {//结点的值大于key，去其左子树进行查找cur=cur.left;}}//没有找到，没有该值return null;}

插入

插入操作可以分为2种情况：当根节点为空时，直接插入到根节点即可；当根节点不为空时，就需要遵守搜索树的性质按照之前查找的逻辑，将节点插入合适的位置，保证不破坏其二叉搜索树的结构；

 public boolean insert (int key){//结点为空，直接进行插入if (root==null){root=new TreeNode(key);return true;}//结点不为空//定义一个cur寻找插入的合适位置TreeNode cur=root;//记录cur的位置或走向TreeNode parent=null;//寻找合适的插入位置，使用parent记录while (cur!=null){if (cur.key<key){parent=cur;cur=cur.right;}else if (cur.key<key){parent=cur;cur=cur.left;}else{//不可以插入相同的数据return false;}}//创建新结点TreeNode node=new TreeNode(key);if (parent.key<key){parent.right=node;}else{parent.left=node;}return true;}

删除

删除操作相较于前面的查找插入操作要略显复杂，大致可以分为下面几种情况：

设待删除的结点为cur，待删除节点的双亲结点为parent；

1. cur.left==null;

cur是root;

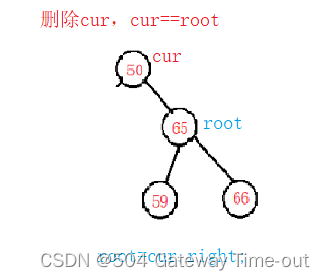
cur不是root,又可以分为2种情况：

cur是其双亲结点parent的左结点：

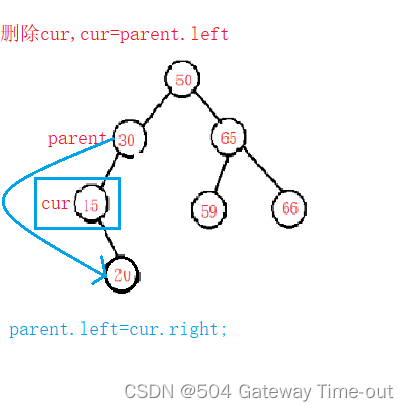
cur是其双亲结点parent的右结点：

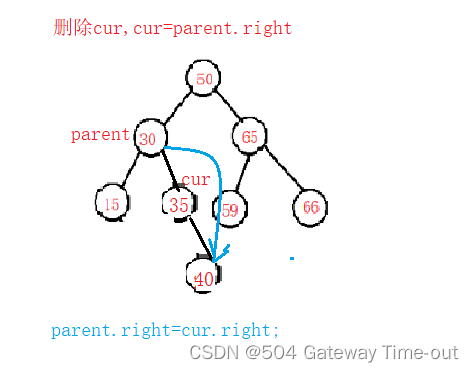
2. cur.right==null;

cur为root；

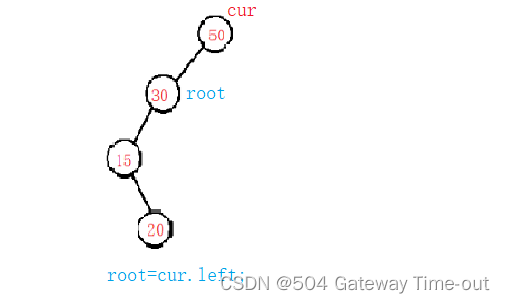
cur不是root,又可以分为2种情况：

cur是其双亲结点parent的左结点：

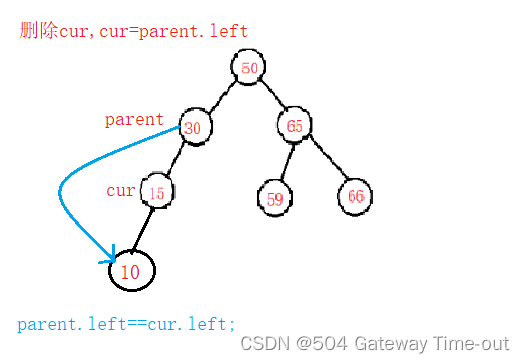
cur是其双亲结点parent的右结点：

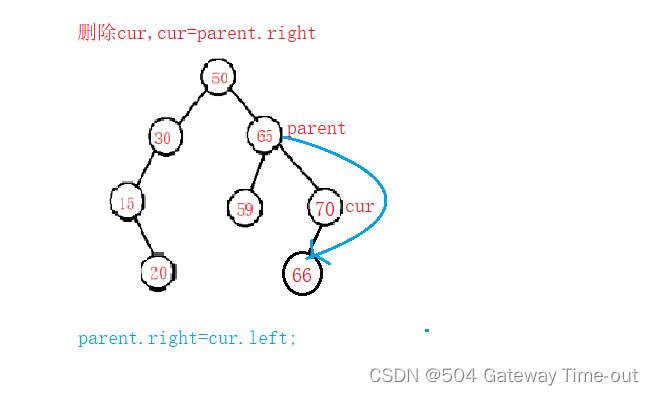
3. cur.left!=null && cur.right!=null;

使用替换法进行删除，使用待删除节点的右子树的最小值将待删除节点进行替换，再删除最小值的结点即可；

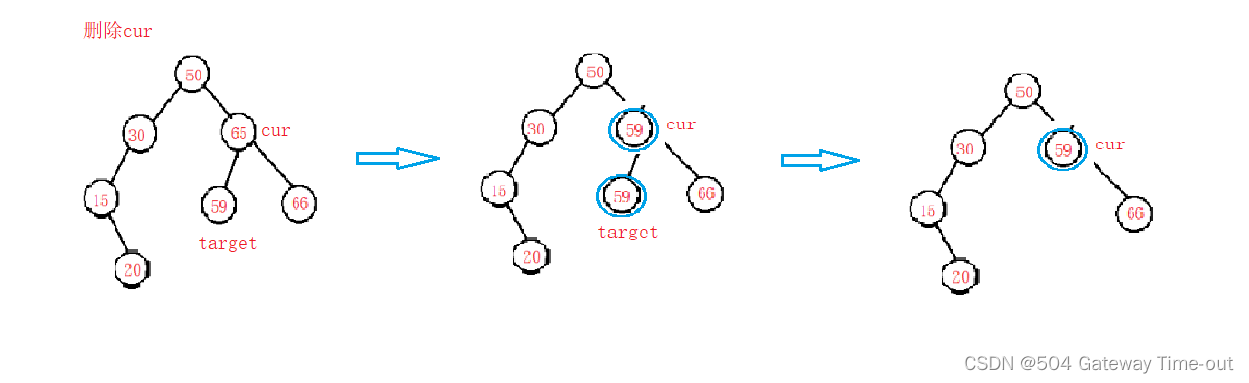
下面是具体的代码实现：

public boolean remove(int key){TreeNode cur=root;TreeNode parent=null;//寻找删除的结点的位置while (cur!=null){if (cur.key<key){parent=cur;cur=cur.right;}else if(cur.key==key){//调用removeNode方法进行具体的删除removeNode(parent,cur);return true;}else{parent=cur;cur=cur.left;}}return false;}private void removeNode(TreeNode parent, TreeNode cur) {//第一种情况if (cur.left==null){if (cur==root){root=cur.right;}else if(cur==parent.left){parent.left=cur.right;}else {parent.right=cur.right;}//第二种情况}else if(cur.right==null){if (cur==root){root=cur.left;}else if(cur==parent.left){parent.left=cur.left;}else {parent.right=cur.left;}}else{//第三种情况，使用替换法TreeNode targetParent=cur;TreeNode target=cur.right;//寻找最小值while (target.left!=null){targetParent=target;target=target.left;}//进行替换cur.key=target.key;//删除那个最小值if (target==targetParent.left){targetParent.left=target.right;}else{targetParent.right=target.right;}}}

对于这样一棵二叉搜索树而言，一般情况下结点所处的位置越深，需要进行比较的次数就越多。因此根据结点插入的次序不同，就可能得到不同结构的二叉树：

最好情况下，得到一棵完全二叉树的结构，平均比较次数达到logN(以2为底)；
最坏情况下，得到一棵单分支树，平均比较次数为N/2;

over!